前言

昨天我們定義價值函數，透過數學家的定義，我們可以找到狀態與動作的價值。不過用手算這個東西很可怕，在 Sutton 書中，第四章開頭處點出有三種方法，可以幫助我們求價值函數。

• 動態規劃 (Dynamic programming)
• 蒙地卡羅方法 (Monte Carlo method)
• Temporal-Difference learning (簡稱 TD learning，我不知道怎麼翻譯比較好)

透過這三種方式的其中一種，我們可以求出價值函數，不過這三種方法各有特色，各自的優缺將會在介紹方法時一併說明。那麼，我們就接續昨天的內容，開始說明第一種求價值函數的方式。

動態規劃

根據昨天提到的內容，我們定義了兩個價值函數，分別如下：

• 狀態價值函數：
• 動作價值函數：

我們需要先改寫一下這個形式，我們才可以使用動態規劃。以下將使用狀態價值函數說明，動作價值函數的推導也差不多，有興趣可以自己試試看。

首先，我們將 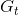代入狀態價值函數，得到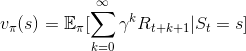

接著，取出第一個回饋 (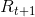)，得到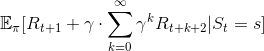

這時候，回想一下離散情況下，期望值的定義。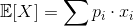

忘記了嗎？沒關係， Google 一下就有了。 [Wikipedia]

把定義帶入價值函數中，得到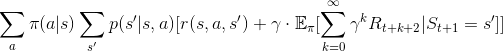

先別急著罵髒話， 這條式子的組成，就是 「機率 x 該機率下的數值」而已，只是條件比較多。

好的，注意一下期望值內的東西，會發現這個東西我們好像有在哪裡看過。

這是狀態價值函數的定義 ()

沒錯，期望值部份就是狀態價值函數的定義，把定義帶進去，得到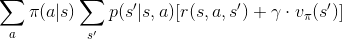

這條數學式又被稱為「貝爾曼方程」。同理，可以推導動作價值函數的貝爾曼方程。

至此，我們已經準備好，要使用動態規劃計算價值函數了。